- 工業簿記を勉強していると固変分解っていう内容が出てきたんだけど……
- 高低点法のやり方が分からない
- 固変分解について教えて!
固変分解は数学的な要素が強いので、数学が苦手な人は固変分解も苦手にしてしまう場合が非常に多いです。
私は簿記通信講座を2012年から運営してきて数百名の合格者をこれまでに送り出させていただきました。もちろん固変分解についても熟知しています。
この記事では簿記2級で出題される固変分解である高低点法を中心に解説します。
この記事を読めば固変分解についてより深く理解できるので、簿記2級で固変分解に関する問題が出題されても自信を持って解答できるようになります。
結論を一言で言うと、固変分解とは、原価を固定費と変動費に分解することです。
固変分解の方法には「勘定科目法(費目別精査法)」「高低点法」「スキャッター・チャート法」「最小自乗法」があります。このうち簿記2級では高低点法を学習します。
固変分解とは:原価を固定費と変動費に分解すること

直接原価計算とCVP分析では、原価を変動費と固定費に分けて計算する必要があります。
原価の分類で変動費と固定費がどのようなものかについてはすでに学習しましたが、現実問題として全ての費用を変動費と固定費に完璧に分類するのは簡単ではありません(というより不可能です)。
完全なる変動費や完全なる固定費ばかりではないからです。電気代や水道代、電話代は変動費のように見えますが、固定費も存在しています。
固定費も一定ではなく、使用量によって変わってきます。消耗品も完全な変動費のようですが、全く使わなくても消耗していく部品もあります。
現実には「これは変動費、これは固定費…」というように完全に分類することが不可能なのです。そこで、簡便に変動費と固定費に分解することになります。
固変分解の4種類の方法

固変分解には4種類の計算方法があります。次のとおりです。
- 勘定科目法(費目別精査法)
- 高低点法(簿記2級)
- スキャッター・チャート法
- 最小自乗法(簿記1級)
勘定科目法(費目別精査法):費目ごとに固定費と変動費に分解する方法
勘定科目法では、過去の経験に基づいて費目ごと(勘定科目ごと)に一つ一つ変動費と固定費に分解していきます。
「これくらい操業度が変わればこれくらい金額が変わる」という過去の経験から分解します。
手間はかかりますし、変動費と固定費の分解が客観的ではないですが、直感的に最も納得しやすい方法なのでよく使われます。
高低点法(簿記2級):最も操業度が多い場合と少ない場合から1次関数を使って求める方法
高低点法は過去の実績データのうち、最も多い操業度のときのデータと最も少ない操業度のときのデータから1次関数のグラフを求めるように変動費率と固定費を求めます。
1次関数でいう傾きが変動費率、切片が固定費になります。
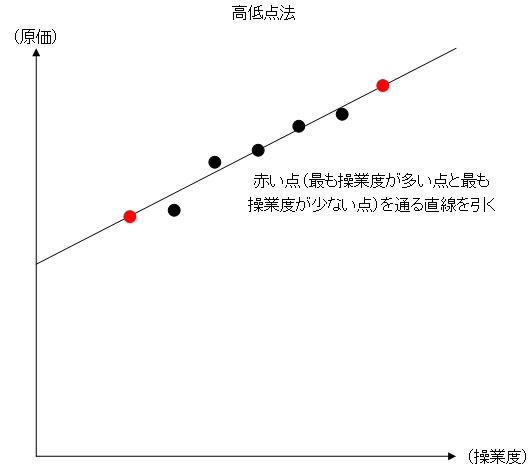
高低点法では最も多い操業度のときのデータと最も少ない操業度のときのデータ以外を全く考えないため、正確性に欠けるというデメリットがあります。
しかし、客観的かつ簡単に変動費率と固定費を求めることができるというメリットがあります。
スキャッター・チャート法:目分量で1次関数を求める方法
原価の過去の実績データをグラフに記入し、データの中心を通る直線を何となく目分量で引いて1次関数のグラフを求めるように変動費率と固定費を求めます。
1次関数でいう傾きが変動費率、切片が固定費になります。
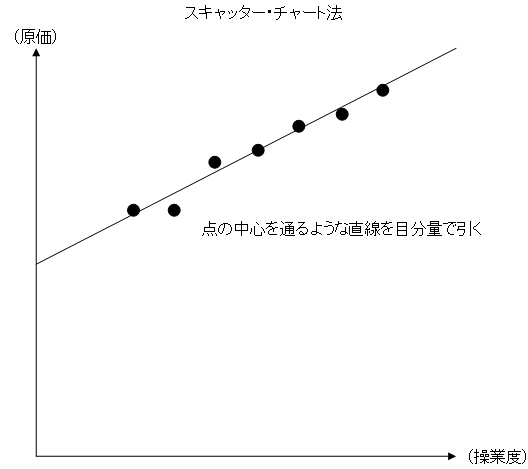
スキャッター・チャート法では計算を行わず感覚で直線を引くので客観的ではないですが、高低点法よりも正確になることが多いと言われています。
最小自乗法(簿記1級):「座標と直線の距離の2乗」の合計が最も小さくなるような1次関数を求める方法
原価の過去の実績データをグラフに記入し、データと直線との距離の2乗の合計が最も小さくなるような直線を求める方法です。
高低点法と同じように客観的に変動費率と固定費を求めることができます。
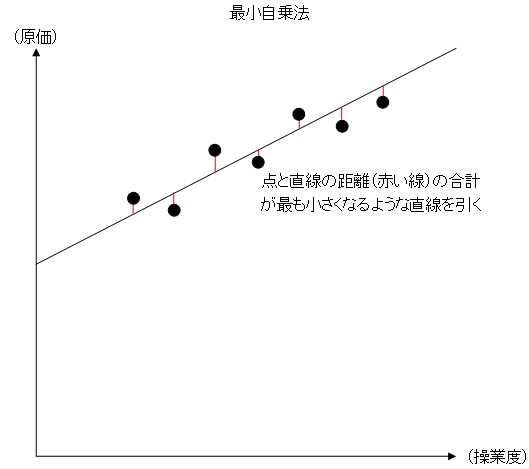
高低点法と比べると最も多い操業度のときのデータと最も少ない操業度のときのデータ以外のデータもきちんと考えるため誤差が小さくなる傾向がありますが、計算そのものは複雑になります。
エクセルなどを使うと計算そのものは自分では行わないため楽ですが、手で計算するのは本当に大変です。
4種類の固変分解の方法の中で簿記2級で出題されるのは高低点法です。高低点法を使って変動費率と固定費を求める方法を身につけることが重要です。
固変分解によって求めた直線は製造間接費予算の公式法変動予算で学習したシュラッター図のように使います。
固変分解(高低点法)の具体例

| 月 | 機械運転時間 | 製造間接費 |
|---|---|---|
| 1 | 1,500hr | 1,330,000円 |
| 2 | 1,300hr | 1,250,000円 |
| 3 | 1,700hr | 1,400,000円 |
| 4 | 1,600hr | 1,370,000円 |
| 5 | 1,400hr | 1,200,000円 |
| 6 | 2,000hr | 1,500,000円 |
| 7 | 2,200hr | 1,700,000円 |
| 8 | 2,800hr | 2,000,000円 |
| 9 | 2,300hr | 1,750,000円 |
| 10 | 2,400hr | 1,800,000円 |
| 11 | 2,100hr | 1,630,000円 |
| 12 | 1,900hr | 1,450,000円 |
この資料により、過去の実績値で最高の操業度と最低の操業度の2点により変動費率と月間の固定費とを求める方法(高低点法)での固変分解を行ってみましょう。
高低点法で固変分解を行う場合、まず最高の操業度の月と最低の操業度の月を見つけ出します。最高は8月、最低は2月です。
| 月 | 機械運転時間 | 製造間接費 |
|---|---|---|
| 2 | 1,300hr | 1,250,000円 |
| 8 | 2,800hr | 2,000,000円 |
原価の推移をy=aχ+b(a:変動費率、b:固定費)とおいて1次関数の直線の式を求めるように解きます。
χが横軸(機械運転時間)、yが縦軸(製造間接費)なので、(1300,1250000)と(2800,2000000)の2点を通る直線の式を求めます。
以下は2点を通る1次関数の式を求める解法です。
χ=1300、y=1250000をy=aχ+bに代入すると、1,250,000=1,300a+b …①
χ=2800、y=2000000をy=aχ+bに代入すると、2,000,000=2,800a+b …②
①-②… -750,000=-1,500a
両辺を-1,500で割る 500=a (変動費率が500円/hrと求まる)
a=500を①に代入する 1,250,000=1,300×500+b
1,300×500を計算する 1,250,000=650,000+b
両辺から650,000を引く 600,000=b (固定費が600,000円と求まる)
直線の式はy=500χ+600,000となります。
- 変動費率…500円/hr
- 固定費…600,000円
このような形で変動費率と固定費を求めます。最高の操業度である月と最低の操業度である月しか考えないため、この2つの月で誤差が大きいと結果も極めて不正確になります。
こういった欠点がありますが、客観的な固変分解の方法の中では最も簡単なので簿記2級ではこの高低点法が出題されます。
【まとめ】固変分解の4種類の方法とは【簿記2級では高低点法で計算】

原価を固定費と変動費に分解することを固変分解と言います。
固変分解の方法には「勘定科目法(費目別精査法)」「高低点法」「スキャッター・チャート法」「最小自乗法」があります。このうち簿記2級では高低点法を学習します。
高低点法で固変分解を行う場合、まず最高の操業度の月と最低の操業度の月を見つけ出します。
そして、原価の推移をy=aχ+b(a:変動費率、b:固定費)とおいて1次関数の直線の式を求めるように解くことでa(変動費率)とb(固定費)を求めます。
- 弊社が運営している【簿記革命2級】は、当サイト「暗記不要の簿記独学講座-商業簿記2級」「暗記不要の簿記独学講座-工業簿記2級」を大幅に加筆修正したテキストと、テキストに完全対応した問題集がセットの通信講座です。私とともに簿記2級や簿記1級の合格を目指して勉強したい方は簿記2級通信講座【簿記革命2級】をご検討ください。
- 簿記2級を効果的に身につけるためには、効果的な勉強方法で勉強することが大切です。簿記2級の勉強法については「簿記1級にラクラク受かる勉強法-簿記2級」で詳しく解説しています。
- 簿記2級の独学に向いたテキストについては「【2021年版】独学向け簿記2級おすすめテキスト【8つのテキストを徹底比較】」で詳しく解説しています。

コメント
大変参考にさせていただいています。ありがとうございます。
一つ気づいたのでコメントします。
本文中に、
最小自乗法
原価の過去の実績データをグラフに記入し、それらのデータと直線との距離の合計が最も小さくなるような直線を求める方法です。
→
それらのデータと直線との距離「の2乗」の合計が最も小さくなるような直線
ではないでしょうか。
自乗(2乗)が最小になるから、最小自乗法ではないかと思います。
コメントありがとうございます。おっしゃるとおりです。最小二乗法では2乗した数値を集計します。ここでは複雑にしたくなかったので(細かい計算は簿記2級では出題されないので)2乗とは書いていませんでしたが、正確さを重視した方がいいと確かに思います。修正させていただきます。